Test for block-indepedence

Function performing a test that evaluates the null hypothesis of block-independence against the alternative of block-dependence (presence of non-zero elements in the off-diagonal block) in the precision matrix using high-dimensional data. The mentioned test is a permutation-based test (see details).

GGMblockTest(
  Y,
  id,
  nPerm = 1000,
  lambda,
  target = default.target(covML(Y)),
  type = "Alt",
  lowCiThres = 0.1,
  ncpus = 1,
  verbose = TRUE
)

Arguments

Y

Data matrix. Variables assumed to be represented by columns.

id

A numeric vector acting as an indicator variable for two blocks of the precision matrix. The blocks should be coded as 0 and 1.

nPerm

A numeric or integer determining the number of permutations.

lambda

A numeric representing the penalty parameter employed in the permutation test.

target

A target matrix (in precision terms) for Type I ridge estimators.

type

A character indicating the type of ridge estimator to be used. Must be one of: "Alt", "ArchI", "ArchII".

lowCiThres

A numeric taking a value between 0 and 1. Determines speed of efficient p-value calculation.

ncpus

A numeric or integer indicating the desired number of cpus to be used.

verbose

A logical indicating if information on progress and output should be printed on screen.

Value

An object of class list:

statistic

A numeric representing the observed test statistic (i.e., likelihood ratio).

pvalue

A numeric giving the p-value for the block-independence test.

nulldist

A numeric vector representing the permutation null distribution for the test statistic.

nperm

A numeric indicating the number of permutations used for p-value calculation.

remark

A "character" that states whether the permutation algorithm was terminated prematurely or not.

Details

The function performs a permutation test for the null hypothesis of block-independence against the alternative of block-dependence (presence of non-zero elements in the off-diagonal block) in the precision matrix using high-dimensional data. In the low-dimensional setting the common test statistic under multivariate normality (cf. Anderson, 2003) is: $$ \log( \| \hat{\mathbf{\Sigma}}_a \| ) + \log( \| \hat{\mathbf{\Sigma}}_b \| ) - \log( \| \hat{\mathbf{\Sigma}} \| ), $$ where the \(\hat{\mathbf{\Sigma}}_a\), \(\hat{\mathbf{\Sigma}}_b\), \(\hat{\mathbf{\Sigma}}\) are the estimates of the covariance matrix in the sub- and whole group(s), respectively.

To accommodate the high-dimensionality the parameters of interest are estimated in a penalized manner (ridge-type penalization, see ridgeP). Penalization involves a degree of freedom (the penalty parameter: lambda) which needs to be fixed before testing. To decide on the penalty parameter for testing we refer to the GGMblockNullPenalty function. With an informed choice on the penalty parameter at hand, the null hypothesis is evaluated by permutation. Hereto the samples are permutated within block. The resulting permuted data set represents the null hypothesis. Many permuted data sets are generated. For each permutation the test statistic is calculated. The observed test statistic is compared to the null distribution from the permutations.

The function implements an efficient permutation resampling algorithm (see van Wieringen et al., 2008, for details.): If the probability of a p-value being below lowCiThres is smaller than 0.001 (read: the test is unlikely to become significant), the permutation analysis is terminated and a p-value of unity (1) is reported.

When verbose = TRUE also graphical output is generated: A histogram of the null-distribution. Note that, when ncpus is larger than 1, functionalities from snowfall are imported.

References

Anderson, T.W. (2003). An Introduction to Multivariate Statistical Analysis, 3rd Edition. John Wiley.

van Wieringen, W.N., van de Wiel, M.A., and van der Vaart, A.W. (2008). A Test for Partial Differential Expression. Journal of the American Statistical Association 103: 1039-1049.

See also

ridgeP, optPenalty.LOOCVauto, default.target, GGMblockNullPenalty

Author

Wessel N. van Wieringen, Carel F.W. Peeters <carel.peeters@wur.nl>

Examples

## Obtain some (high-dimensional) data
p = 15
n = 10
set.seed(333)
X = matrix(rnorm(n*p), nrow = n, ncol = p)
colnames(X)[1:15] = letters[1:15]
id <- c(rep(0, 10), rep(1, 5))

## Generate null distribution of the penalty parameter
lambda0dist <- GGMblockNullPenalty(X, id, 5, 0.001, 10)

## Location of null distribution
lambdaNull <- median(lambda0dist)

## Perform test
testRes <- GGMblockTest(X, id, nPerm = 100, lambdaNull)
#> 0 of 100 permutations done, and counting...
#> 25 of 100  permutations done 
#> 25 of 100 permutations done, and counting...
#> 50 of 100  permutations done 
#> 50 of 100 permutations done, and counting...

#> 
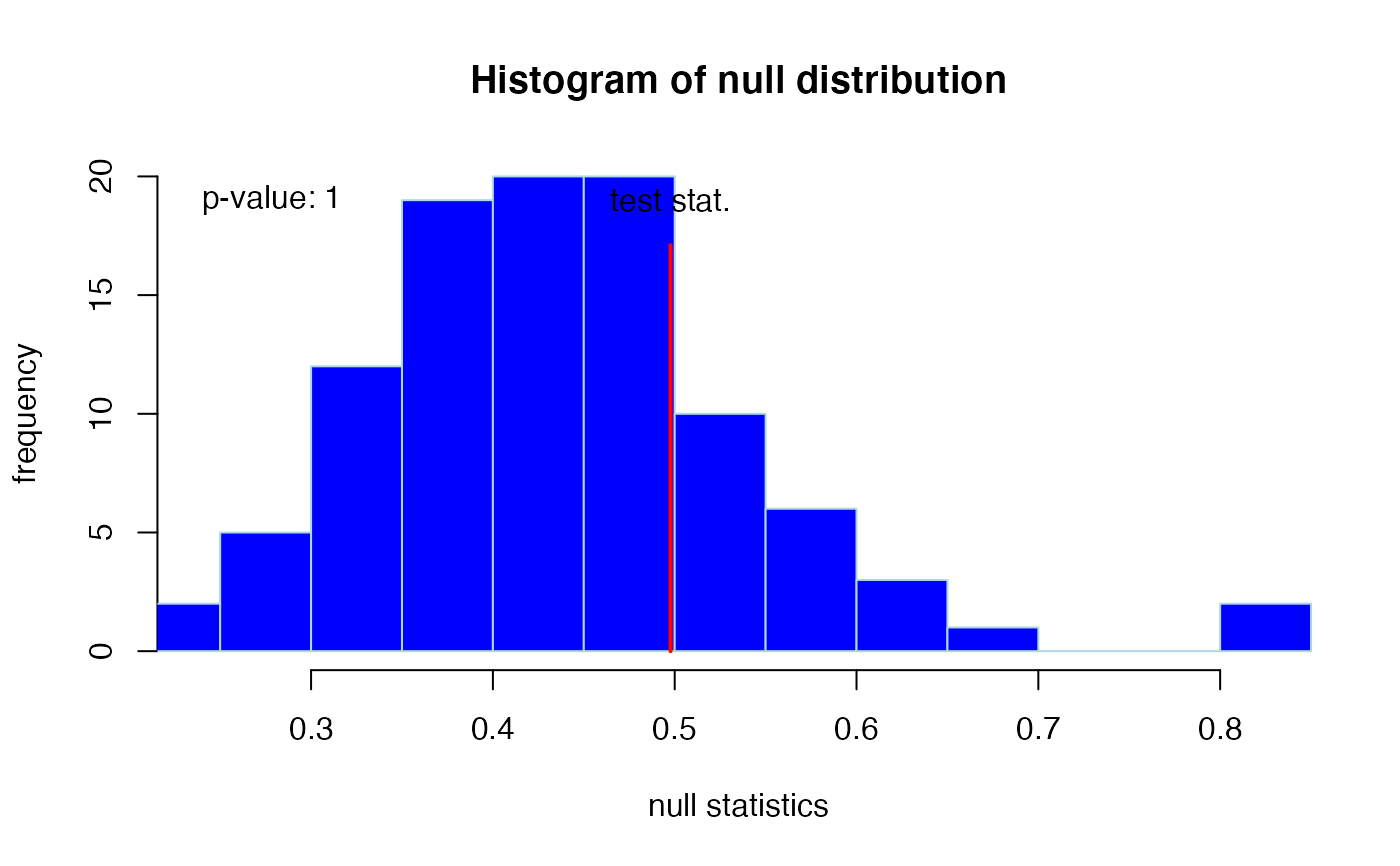#> Likelihood ratio test for block independence
#> ----------------------------------------
#> -> number of permutations : 100
#> -> test statistic         : 0.498
#> -> p-value                : 1
#> -> remark                 : resampling terminated prematurely due to unlikely significance
#> ----------------------------------------
#>