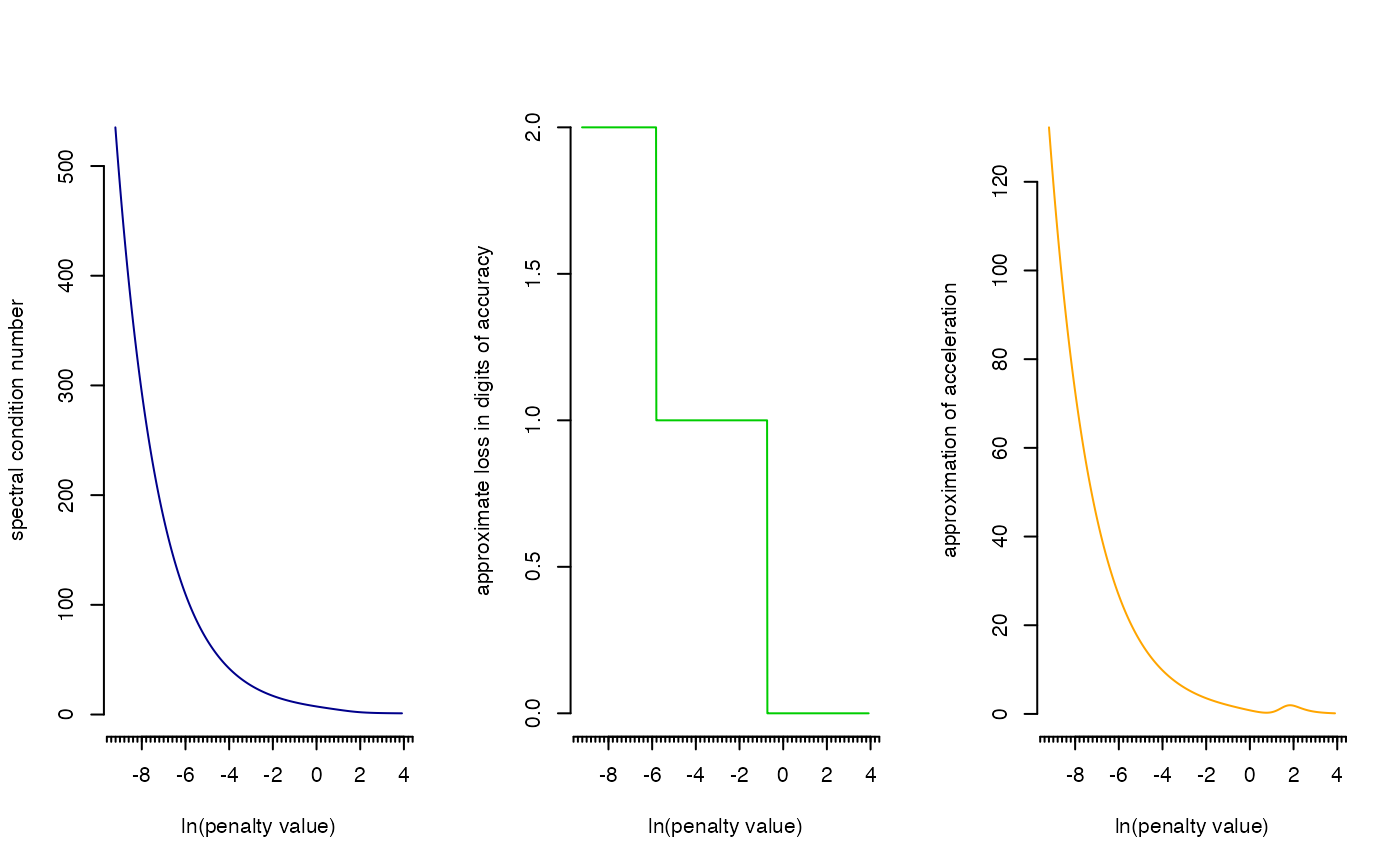
Visualize the spectral condition number against the regularization parameter

Function that visualizes the spectral condition number of the regularized precision matrix against the domain of the regularization parameter. The function can be used to heuristically determine an acceptable (minimal) value for the penalty parameter.

CNplot(
  S,
  lambdaMin,
  lambdaMax,
  step,
  type = "Alt",
  target = default.target(S, type = "DUPV"),
  norm = "2",
  Iaids = FALSE,
  vertical = FALSE,
  value = 1e-100,
  main = "",
  nOutput = FALSE,
  verbose = TRUE,
  suppressChecks = FALSE
)

Arguments

S: Sample covariance matrix.
lambdaMin: A numeric giving the minimum value for the penalty parameter.
lambdaMax: A numeric giving the maximum value for the penalty parameter.
step: An integer determining the number of steps in moving through the grid [lambdaMin, lambdaMax].
type: A character indicating the type of ridge estimator to be used. Must be one of: "Alt", "ArchI", "ArchII".
target: A target matrix (in precision terms) for Type I ridge estimators.
norm: A character indicating the norm under which the condition number is to be calculated/estimated. Must be one of: "1", "2".
Iaids: A logical indicating if the basic condition number plot should be amended with interpretational aids.
vertical: A logical indicating if output graph should come with a vertical line at a pre-specified value for the penalty parameter.
value: A numeric indicating a pre-specified value for the penalty parameter.
main: A character with which to specify the main title of the output graph.
nOutput: A logical indicating if numeric output should be returned.
verbose: A logical indicating if information on progress should be printed on screen.
suppressChecks: A logical indicating if the input checks should be suppressed.

Value

The function returns a graph. If nOutput = TRUE the function also returns an object of class list:

lambdas: A numeric vector representing all values of the penalty parameter for which the condition number was calculated. The values of the penalty parameter are log-equidistant.
conditionNumbers: A numeric vector containing the condition number for each value of the penalty parameter given in lambdas.

Details

Under certain target choices the proposed ridge estimators (see ridgeP) are rotation equivariant, i.e., the eigenvectors of \(\mathbf{S}\) are left intact. Such rotation equivariant situations help to understand the effect of the ridge penalty on the precision estimate: The effect can be understood in terms of shrinkage of the eigenvalues of the unpenalized precision estimate \(\mathbf{S}^{-1}\). Maximum shrinkage implies that all eigenvalues are forced to be equal (in the rotation equivariant situation). The spectral condition number w.r.t. inversion (ratio of maximum to minimum eigenvalue) of the regularized precision matrix may function as a heuristic in determining the (minimal) value of the penalty parameter. A matrix with a high condition number is near-singular (the relative distance to the set of singular matrices equals the reciprocal of the condition number; Demmel, 1987) and its inversion is numerically unstable. Such a matrix is said to be ill-conditioned. Numerically, ill-conditioning will mean that small changes in the penalty parameter lead to dramatic changes in the condition number. From a numerical point of view one can thus track the domain of the penalty parameter for which the regularized precision matrix is ill-conditioned. When plotting the condition number against the (domain of the) penalty parameter, there is a point of relative stabilization (when working in the \(p > n\) situation) that can be characterized by a leveling-off of the acceleration along the curve when plotting the condition number against the (chosen) domain of the penalty parameter. This suggest the following fast heuristic for determining the (minimal) value of the penalty parameter: The value of the penalty parameter for which the spectral condition number starts to stabilize may be termed an acceptable (minimal) value.

The function outputs a graph of the (spectral) matrix condition number over the domain [lambdaMin, lambdaMax]. When norm = "2" the spectral condition number is calculated. It is determined by exact calculation using the spectral decomposition. For most purposes this exact calculation is fast enough, especially when considering rotation equivariant situations (see ridgeP). For such situations the amenities for fast eigenvalue calculation as provided by RSpectra are used internally. When exact computation of the spectral condition number is deemed too costly one may approximate the computationally friendly L1-condition number. This approximation is accessed through the rcond function (Anderson et al. 1999).

When Iaids = TRUE the basic condition number plot is amended/enhanced with two additional plots (over the same domain of the penalty parameter as the basic plot): The approximate loss in digits of accuracy (for the operation of inversion) and an approximation to the second-order derivative of the curvature in the basic plot. These interpretational aids can enhance interpretation of the basic condition number plot and may support choosing a value for the penalty parameter (see Peeters, van de Wiel, & van Wieringen, 2016). When vertical = TRUE a vertical line is added at the constant value. This option can be used to assess if the optimal penalty obtained by, e.g., the routines optPenalty.LOOCV or optPenalty.aLOOCV, has led to a precision estimate that is well-conditioned.

Note

The condition number of a (regularized) covariance matrix is equivalent to the condition number of its corresponding inverse, the (regularized) precision matrix. Please note that the target argument (for Type I ridge estimators) is assumed to be specified in precision terms. In case one is interested in the condition number of a Type I estimator under a covariance target, say \(\mathbf{\Gamma}\), then just specify target = solve(\(\mathbf{\Gamma}\)).

References

Anderson, E, Bai, Z., ..., Sorenson, D. (1999). LAPACK Users' Guide (3rd ed.). Philadelphia, PA, USA: Society for Industrial and Applied Mathematics.

Demmel, J.W. (1987). On condition numbers and the distance to the nearest ill-posed problem. Numerische Mathematik, 51: 251--289.

Peeters, C.F.W., van de Wiel, M.A., & van Wieringen, W.N. (2020). The spectral condition number plot for regularization parameter evaluation. Computational Statistics, 35: 629--646.

Author

Carel F.W. Peeters <carel.peeters@wur.nl>

Examples


## Obtain some (high-dimensional) data
p = 25
n = 10
set.seed(333)
X = matrix(rnorm(n*p), nrow = n, ncol = p)
colnames(X)[1:25] = letters[1:25]
Cx <- covML(X)

## Assess spectral condition number across grid of penalty parameter
CNplot(Cx, lambdaMin = .0001, lambdaMax = 50, step = 1000)
#> Perform input checks... 
#> Calculating spectral condition numbers... 
#> Plotting... 

## Include interpretational aids
CNplot(Cx, lambdaMin = .0001, lambdaMax = 50, step = 1000, Iaids = TRUE)
#> Perform input checks... 
#> Calculating spectral condition numbers... 
#> Calculating interpretational aids... 
#> Plotting...