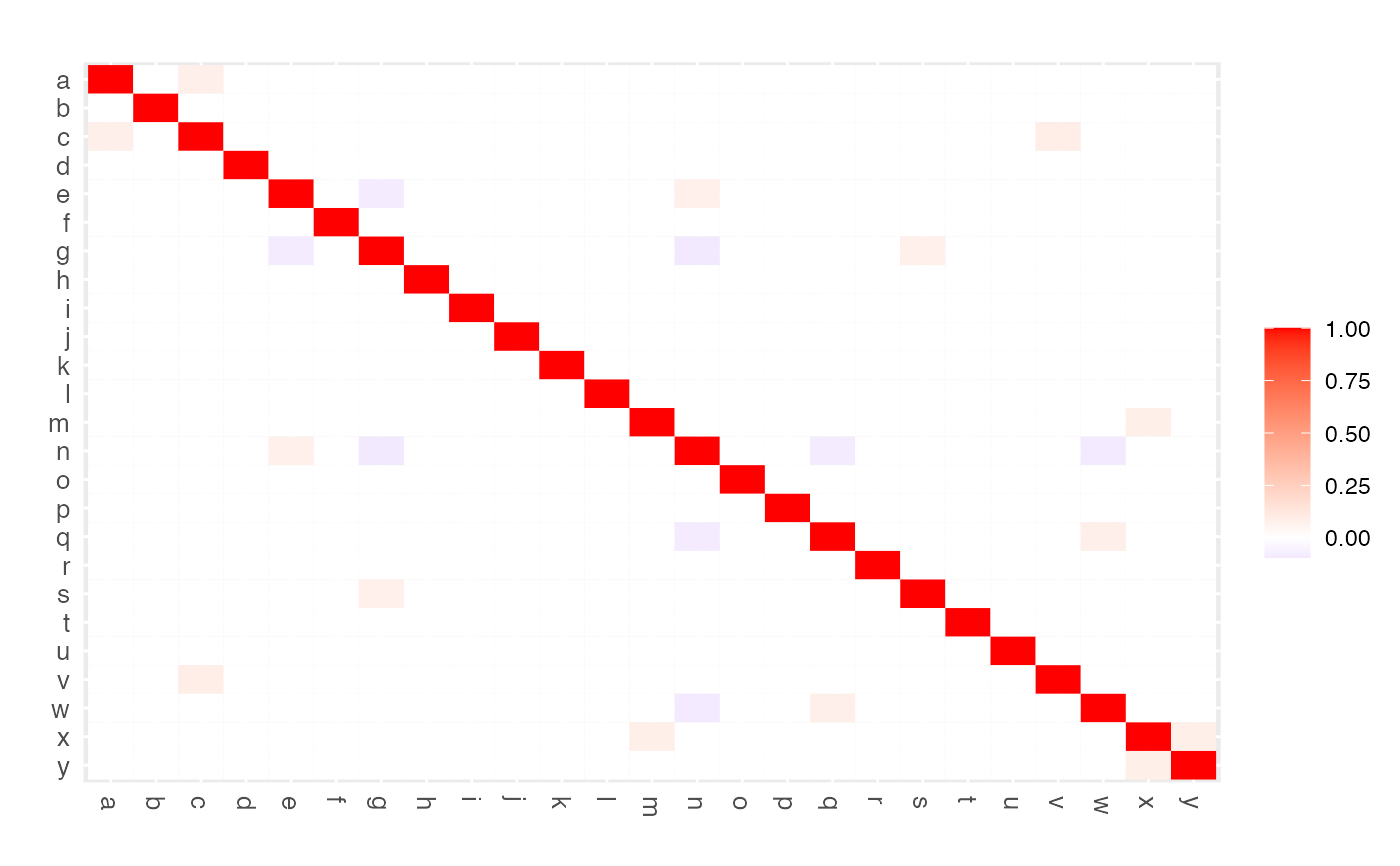
Visualize (precision) matrix as a heatmap

Function that visualizes a (precision) matrix as a heatmap. May be used to assess visually the elements of a single (possibly sparsified precision) matrix. May also be used in assessing the performance of edge selection techniques.

edgeHeat(
  M,
  lowColor = "blue",
  highColor = "red",
  textsize = 10,
  diag = TRUE,
  legend = TRUE,
  main = ""
)

Arguments

M: (Possibly sparsified precision) matrix.
lowColor: A character that determines the color scale in the negative range.
highColor: A character that determines the color scale in the positive range.
textsize: A numeric scaling the text size of row and column labels.
diag: A logical determining if the diagonal elements of the matrix should be included in the color scaling. This argument is only used when M is a square matrix.
legend: A logical indicating whether a color legend should be included.
main: A character giving the main figure title.

Details

This function utilizes ggplot2 (Wickham, 2009) to visualize a matrix as a heatmap: a false color plot in which the individual matrix entries are represented by colors. lowColor determines the color scale for matrix entries in the negative range. highColor determines the color scale for matrix entries in the positive range. For the colors supported by the arguments lowColor and highColor, see https://stat.columbia.edu/~tzheng/files/Rcolor.pdf. White entries in the plot represent the midscale value of 0. One can opt to set the diagonal entries to the midscale color of white when one is interested in (heatmapping) the off-diagonal elements only. To achieve this, set diag = FALSE. Naturally, the diag argument is only used when the input matrix M is a square matrix.

The intended use of the function is to visualize a, possibly sparsified, precision matrix as a heatmap. The function may also be used, in a graphical modeling setting, to assess the performance of edge selection techniques. However, the function is quite general, in the sense that it can represent any matrix as a heatmap.

References

Wickham, H. (2009). ggplot2: elegant graphics for data analysis. New York: Springer.

Author

Carel F.W. Peeters <carel.peeters@wur.nl>, Wessel N. van Wieringen

Examples


## Obtain some (high-dimensional) data
p = 25
n = 10
set.seed(333)
X = matrix(rnorm(n*p), nrow = n, ncol = p)
colnames(X)[1:25] = letters[1:25]
Cx <- covML(X)

## Obtain regularized precision matrix
P <- ridgeP(Cx, lambda = 10, type = "Alt")

## Obtain sparsified partial correlation matrix
PC0 <- sparsify(P, threshold = "localFDR", FDRcut = .8)$sparseParCor
#> Step 1... determine cutoff point
#> Step 2... estimate parameters of null distribution and eta0
#> Step 3... compute p-values and estimate empirical PDF/CDF
#> Step 4... compute q-values and local fdr
#> Step 5... prepare for plotting

#> 
#> - Retained elements:  11 
#> - Corresponding to 3.67 % of possible edges 
#>  

## Visualize sparsified partial correlation matrix as heatmap
edgeHeat(PC0)
#> Warning: 'as.is' should be specified by the caller; using TRUE
#> Warning: 'as.is' should be specified by the caller; using TRUE